STD IX – PURE ARITHMETICS- (Online)
About Course
In this Section we will Learn the following Chapters:
1.RATIONAL NUMBERS
2.IRRATIONAL NUMBERS
Last Updated:March 31, 2022
0 (0 Ratings)
Share Course
Page Link
Share on social media
Description
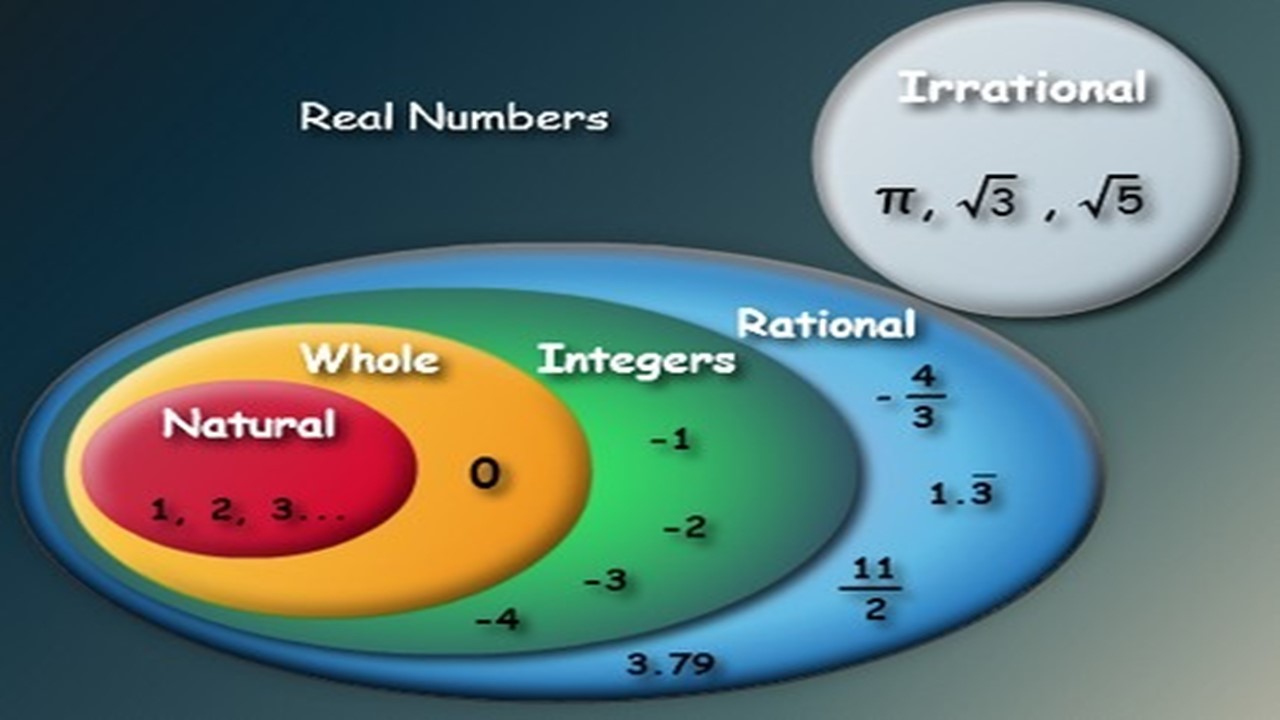
RATIONAL AND IRRATIONAL NUMBERS
RATIONAL NUMBERS
Rational numbers are real numbers that can be expressed as a fraction where the numerator and the denominator of the fraction are both integers. This includes all whole numbers (for example, 3 be written as 3/1) and all finite or recurring decimals.
Rational Numbers
Any number which can be put in the form of pqwhere p and q are integers and q not equal to zero is called a rational number.
There exist an infinite number of rational numbers between any two rational numbers
For example, in between 7 and 7.5 there exist 7.1, 7.11, 7.21, etc.)
A fraction is a rational number only when it is in its lowest form, i.e., there is no common factor other than 1 in the numerator (p) and denominator (q)
Algebraic operations on rational numbers
Sum of two rational numbers is a rational number
Difference of two rational numbers is a rational number
Product of two rational numbers is a rational number
Quotient of two rational numbers is a rational number
Free
Free
Free access this course
-
LevelIntermediate
-
Last UpdatedMarch 31, 2022
-
CertificateYes
Hi, Welcome back!
Material Includes
-
Live Interactive classes with in-class doubt solving
-
Weekly Test and Quiz with instant tracking for progress
-
Revision of the course after testing
-
Fortnightly Parents and Tutor interactions
-
Expert monitoring of student's learning progress
-
Daily communication over call, whatsapp and mail
-
3 hours on-demand video
-
4 downloadable resources
-
Access for entire Academic Year
-
Access on mobile and Desktop
-
Assignments and review of the same
-
Tests and Correction by Board paper checkers
-
Certificate of completion and Live tracking with Grade book
Course Duration:
0
Course level:Intermediate
Enrolled:0
About Course
In this Section we will Learn the following Chapters:
1.RATIONAL NUMBERS
2.IRRATIONAL NUMBERS
Course Curriculum
RATIONAL NUMBERS AND IRRATIONAL NUMBERS
-
06:00
-
05:00
-
QUIZ – RATIONAL NUMBERS
-
QUIZ – PROPERTIES OF RATIONAL NUMBERS
-
05:00
-
01:56
-
QUIZ – IRRATIONAL NUMBERS
-
QUIZ – DECIMAL REPRESENTATION OF RATIONAL NUMBERS
-
QUIZ – RATIONAL NUMBER – NUMBER SYSTEM
-
QUIZ – RATIONAL NUMBER – REAL NUMBERS
-
QUIZ – RATIONAL NUMBER – INTRODUCTION TO RATIONAL NUMBERS
-
QUIZ – RATIONAL NUMBER – PROPERTIES OF RATIONAL NUMBERS
-
QUIZ – EXERCISE A – PROPERTIES OF RATIONAL NUMBERS
-
QUIZ – EXERCISE B – DECIMAL REPRESENTATION OF RATIONAL NUMBERS
-
QUIZ – EXERCISE C – IDENTIFYING REAL NUMBERS
-
QUIZ – EXERCISE D – RATIONALISE THE DENOMINATOR
-
EXERCISE D – RATIONALISATION OF SURDS
Student Ratings & Reviews

No Review Yet

